欧拉发现在多面体的顶点、边与面的数目间存在着一种简单的关系,这种关系被视为图论(graph theory)中相当重要的定理。
你现在应该可以自己叙述欧拉关系了。看看此关系是否也能适用于其他的多面体,检验一下你的推论。
当时欧拉认为这只是多面体的性质,但后来数学家发现这种关系也能适用于球面或平面上的网络。
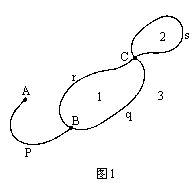
考虑如图1的网络。其中有3个结点A、B、C,4条弧p、q、r、s;这个网络把平面分成3个区域1、2、3.这些数目满足下列关系:
N-A+R=2
N为结点的数目,A为弧的数目,R为区域的数目。你觉得这与多面体的关系是否有什么类似之处?
现在把上述的关系式用在其他的网络上,试试结果如何。
你是否试过图2中不相连的网络?
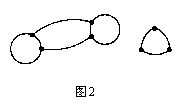
你应该会发现,上述的关系式需要视网络中分离部分的数目作修正。看看你是否能找到一个公式,不管网络中到底有多少部分,都能成立。
“欧拉关系”与“网络关系”之间的联系可以用图3说明。
想象一下,用具有弹性的材料做一个立方体,可以如图3的方式伸展,然后压平,成为平面上的网络。原来立方体的每一个顶点现在都成为网络中的结点,原来立方体的每一条边现在则成为网络中的一条弧。

立方体的每一面现在都成为平面中的一个区域,只除了ABCD之外,不过也可以把ABCD看成是代表网络外部的区域。所有多面体以这种方式变换都可得到类似的结果,但要注意的是,对有洞的多面体需要做进一步的考察。
如果将多面体看作是三维空间分隔成不同区域,则对欧拉的关系式还可以作进一步推广。
考虑一下最简单的多面体——四面体(图4)。
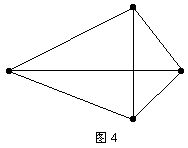
四面体将空间分成两个区域,且
V-E+F-R=4-6+4-2=0
其中V、E、F各代表多面体的顶点、边与面的数目,R为区域的数目。现在在立方体上加一个金字塔形的角锥体。这种组合将空间分成3个区域,包括9个顶点、16条边与10个面(图5)。
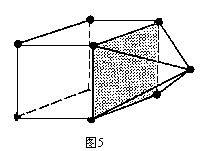
我们再度得出
V-E+F-R=0
这是由欧拉原始的关系式推广得出的另一个关系式。用其他的方法分割空间,检验一下这个关系式。

